This website serve as an interative tool to visualize transformer model by its latent space. The detail of the method is explained in this paper. Code is available at Here
Introduction
Word embedding vectors can be factorized into a sparse linear combination of word factors
\begin{align*} % \vspace{-0.2in} \text{apple} =& 0.09``\text{dessert}" + 0.11``\text{organism}" + \\ & 0.16``\text{fruit}" + 0.22``\text{mobile&IT}" + 0.42``\text{other}". \end{align*}
We view the latent representation of words in a transformer as contextualized word embedding. Similarly, our hypothesis is that a contextualized word embedding vector can also be factorized as a sparse linear superposition of a set of elementary elements, which we call transformer factors.
We feed many sentences into a transformer model. Then we collect the hidden state for each word from each layers. Let $X$ be set of hidden states from different layers, $\forall x \in X$, we assume $x$ is a sparse linear superposition of transformer factors: $$\label{sparse} x = \Phi \alpha + \epsilon, \ s.t. \ \alpha \succeq 0, $$
where $\Phi\in{\rm I\!R}^{d\times m}$ is a dictionary matrix with columns $\Phi_{:,c}\ $, $\alpha \in{\rm I\!R}^m$ is a sparse vector of coefficients to be inferred and $\epsilon$ is a vector containing independent Gaussian noise samples, which are assumed to be small relative to $x$. Each column $\Phi_{:,c}\ $ of $\Phi$ is a transformer factor and its corresponding sparse coefficient $\alpha_c$ is its activation level.
How the dictionary is learned is explained in the paper. Transformer factors $\Phi_{:,c}$
are divided into three different levels: low level, mid level and high level:
Low level transformer factors correspond to word-level disambiguation.
Mid level transformer factors correspond to sentence-level patterns.
High level transformer factors correspond to long range patterns.
The details on how to divide those transformer factors into three levels is also explained in the paper.
Visualization
In the following box, input a number $c$ indicating the transformer factor $\Phi_{:,c}$ you want to visualize. Then click the button "" to visualize this transformer factor at a particular layer. For a transformer factor $\Phi_{:,c}$ and for a layer-$l$, the visualization is done by listing the 200 word and context with the largest sparse coefficients $\alpha^{(l)}_c$'s
← Enter an integer from 0 to 531, indicating the transformer factor you want to visualize.
Alternatively, you can click the three buttom below to get a random low level, mid level or high level transformer factor:
← (We generate saliency map for high level transformer factor using LIME)
*
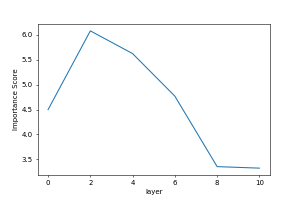
This is the "importance score" for this transformer factor. The importance score reflects the average activation of this transformer factor in different layers.